| Level: |
MSc |
| Title: |
Vibrating plates and magnetic fluxes |
| Supervisor: |
|
| Research Area: |
Dynamical Systems and Statistical Physics |
| Description: |
A quick search on youtube for ‘Chladni plate’ will return numerous wonderful videos displaying the beautiful images that are created when sand is poured over a vibrating metal plate. By tuning the frequency, one can excite the various resonances 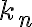 of the plate and ‘see’ how it vibrates - a technique first of the plate and ‘see’ how it vibrates - a technique first
demonstrated by Chladni using a violin bow. Mathematically, this corresponds to finding the solutions to the Helmholtz equation. The project will be to first understand and compute these solutions using finite difference methods (a basic understanding in Matlab or other similar programming language is therefore required). This will be done for various shapes of plates. Afterwards the aim is to apply the same methods to the Aharanov-Bohm modified equation with one or more flux lines. For further details of the project see this document.
|
| Further Reading: |
- W. F. Ames, Numerical methods for partial differential equations. Third edition. Academic press, 2014.
- G. Date, S. R. Jain, M. V. N. Murthy, Rectangular billiard in the presence of a flux line, Phys. Rev. E 51 (1995) 198–203.
- S. Rahav, S. Fishman, Spectral statistics of the rectangular billiard with a flux line, Foundations of Physics 31 (2001) 115–146.
|
| Key Modules: |
|
| Other Information: |
The project requires basic background knowledge of multivariate calculus and PDEs, linear algebra, and computational methods.
|
| Current Availability: |
Yes |
| |