| Description: |
This project is suitable for someone with an interest in Group Theory and Combinatorics.
According to the Classification of Finite Simple Groups (normally abbreviated to CFSG) each finite simple group belongs to (at least) one of the following classes:
- The cyclic groups
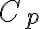 of prime order; of prime order;
- The alternating groups
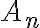 of degree at least 5; of degree at least 5;
- Six families of classical groups, parameterised by dimension and field (size);
- Ten families of exceptional groups of Lie type, parameterised by field; and
- Some 26 or 27 sporadic groups (depending on whether you count the Tits group
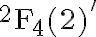 as sporadic). as sporadic).
Five of the sporadic groups were discovered in the 1860s and 1870s by Émile Mathieu, and named after him; we shall be studying these groups, and their subgroups. We shall also be studying objects associated with these groups, such as various Steiner systems and certain codes. One aim is to prove the uniqueness of certain Steiner systems such as 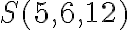 . .
For a proper understanding of the Mathieu groups, it is also necessary to study the exceptional behaviour of certain alternating and linear 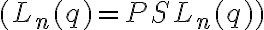 groups, including exceptional isomorphisms, actions, and automorphism groups. For example the symmetric group groups, including exceptional isomorphisms, actions, and automorphism groups. For example the symmetric group 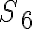 has an exceptional (outer) automorphism. Another aim will be to study this behaviour also (proving some exceptional isomorphisms, etc). has an exceptional (outer) automorphism. Another aim will be to study this behaviour also (proving some exceptional isomorphisms, etc).
|
| Further Reading: |
- J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker, R. A. Wilson, An ATLAS of Finite Groups. Corrected reprint of the 1985 edition. Clarendon Press, Oxford, 2003.
- Sphere Packings, Lattices and Groups (3rd Edition), Chapters 10 and 11. Ed by J. H. Conway and N. J. A. Sloane. Springer-Verlag, New York, 1999.
- R. T. Curtis, The Steiner system
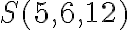 , the Mathieu group , the Mathieu group 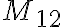 and the "kitten", in Computational group theory (Durham, 1982), Edited by M. D. Atkinson, 353–358, Academic Press, London, 1984. and the "kitten", in Computational group theory (Durham, 1982), Edited by M. D. Atkinson, 353–358, Academic Press, London, 1984.
- R. L. Griess, Twelve sporadic groups. Springer Monographs in Mathematics, Springer-Verlag, Berlin, 1998.
- J. F. Humphreys, A course in group theory. Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1996.
- R. A. Wilson, Finite simple groups. Graduate Texts in Mathematics, Vol. 251, Springer-Verlag, London, 2009.
|