Maths Project Repository Database

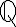
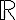
1- Hasse-Minkowski principle. The theorem of Hasse and Minkowski states, roughly, that for a quadratic equation with rational coefficients to have a solution in $\mathbb{Q}$ it is necessary and sufficient that it has solutions at every prime and also in $\mathbb{R}$. This theorem has deep links with Number Theory.

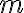
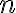
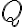
2- Pfister forms and multiplicativity. A theorem of Fermat states that if integers $m$ and $n$ are of the form $x^2+y^2$, then so is $mn$. Lagrange proved the same statement for $x^2+y^2+z^2+t^2$.  Pfister generalized this to the case with $2^k$ variables and proved the similar statement over any field. In fact, he characterized all quadratic forms $Q$ with an analogous multiplicativity property, leading to the theory of the so-called Pfister forms.

3- Structure of the Witt Ring.  The proper understanding of quadratic forms requires studying the so-called Witt ring and its analogue, the Grothendieck-Witt ring.   Pfister forms play a crucial role here. These rings turn out to have deep connections to Algebraic Geometry, Galois Theory and K-theory.  Vladimir Voevodsky was awarded a Fields medal for his work on this subject.

4- Clifford algebras. To any quadratic form one associates a Clifford algebra. These were invented by the Birtish mathematician William Kingdom Clifford in 1878 as a generalization of Hamilton's Quaternion algebras. They have an interesting structure whose study can be part of a nice thesis (for example: classification of Clifford algebras).  Clifford algebras play an important role in Geometry and Physics.