Four dimensional space is fundamentally different to every other dimension. For example, however messily you embed a rectangle in the plane, you can always draw a smooth curve (without sharp turns) between a pair of opposite edges, inside the rectangle (e.g. the red curve below).
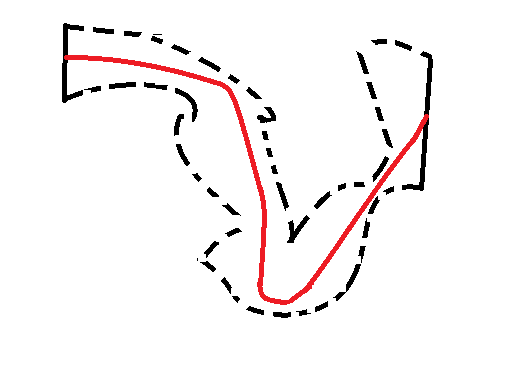
This is essentially because all 2d rectangles are the same as far as differentiation is concerned. This is also true for the analogues of rectangles in dimension 3 and all dimensions from 5 and above. However in dimension 4 one might embed a hypercuboid in such a strange way that no smooth disk can cut across opposite faces.
These 'exotic' shapes were first discovered in the 1980's and earned the discoverer a Fields medal (the highest accolade in mathematics). His approach involved considering instantons; solutions to the Yang-Mills equations from particle physics.
In 2004 a much simpler and purely combinatorial approach was discovered. This involves considering circular strings floating through 4-d space-time and the surfaces they trace out as they split and combine. One regards these strings as being in a quantum superposition of states (say positive and negative), which allows us to extract an algebraic structure known as a chain complex.
The aim of this project is to follow this more modern approach. As the subject is relatively young, you should be able to get up to fairly recent ideas quite quickly. Not much will be needed in terms of prerequisites (just a strong grasp of linear algebra: vector spaces, linear maps, kernels, rank etc.).
The paper [1] below is a friendly introduction to some of the key ideas. This is built on in [4]. The web book [3] provides some background on spectral sequences and [2] may give you a feel for topological quantum field theory.