Galois theory studies solutions to polynomial equations by looking at how various roots of a polynomial are related to each other. More precisely, the structure of the field extensions obtained by adjoining roots of a polynomial are studied via the group
of symmetries of the roots. This provides a link between field theory and group theory, which culminates in Galois theorem establishing a bijective correspondence between intermediate fields of a Galois field extension 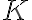 and subgroups of the
Galois group
and subgroups of the
Galois group 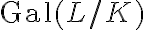 .
.
Differential Galois theory (or Picard-Vessiot theory) uses similar ideas to study solutions to homogenous linear differential equations. An ordinary field is now replaced by a field 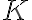 equipped with a notion of differentiation, and the goal is to study
the space of solutions of a differential equation (in a larger differential field
equipped with a notion of differentiation, and the goal is to study
the space of solutions of a differential equation (in a larger differential field 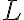 containing
containing 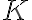 , the "Picard-Vessiot extension"). The differential Galois theorem establishes a bijective correspondence between intermediate differential fields
of a Picard-Vessiot extension
, the "Picard-Vessiot extension"). The differential Galois theorem establishes a bijective correspondence between intermediate differential fields
of a Picard-Vessiot extension 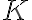 and closed subgroups of its differential Galois group
and closed subgroups of its differential Galois group 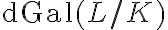 .
.
The goal of this project is to work towards the proof of the differential Galois correspondence, and work out some explicit examples along the way. Possible related topics include Liouville's theorem and Risch's algorithm for indefinite integration.